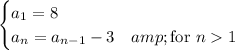Question

In an arithmetic sequence, a_17 = -40 and a_28 = -73. Please explain how to use this information to write a recursive formula for this sequence!

Answer 1

An arithmetic sequence

`a_1,a_2,a_3,\ldots,a_n,\ldots`

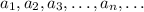
is one in which consecutive terms of the sequence differ by a fixed number, call it d. This means that, given the first term
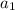`a_1`, we can build the sequence by simply adding d :

`a_2=a_1+d`

`a_3=a_2+d`

`a_4=a_3+d`

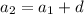
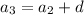
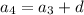
and so on, the general pattern governed by the recursive rule,

`a_n=a_(n-1)+d`

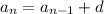
We can exploit this rule in order to write any term of the sequence in terms of the first one. For example,

`a_3=a_2+d=(a_1+d)+d=a_1+2d`

`a_4=a_3+d=(a_1+2d)+d=a_1+3d`

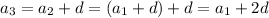
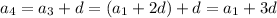
and so on up to

`a_n=a_1+(n-1)d`

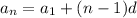
In this case, we're not given the first term right away, but the 17th. But this isn't a problem; we can use the same exploit to get

`a_(18)=a_(17)+d`

`a_(19)=a_(17)+2d`

`a_(20)=a_(17)+3d`

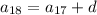
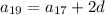
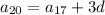
and so on, up to the next term we know,

`a_(28)=a_(17)+11d=-40+11d`

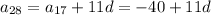
(Notice how the subscript of a on the right and the coefficient of d add up to the subscript of a on the left.)

The 28th term is -73, so we can solve for d :

`-73=-40+11d\implies -33=11d\implies d=-3`

To get the first term of the sequence, we use the rule found above and either of the known values of the sequence. For instance,

`a_(17)=a_1+16d\implies-40=a_1-16\cdot3\implies a_1=8`

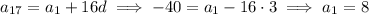
Then the recursive rule for this particular sequence is

`\begin{cases}a_1=8\\a_n=a_(n-1)-3&\text{for }n>1\end{cases}`