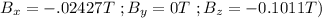Answer:
Step-by-step explanation:
Given that :
The current I = 8.6 A
The length vector L = 2.3 m i
The force vector is = -2.0 j N
When L = 2.3 m i ; the
Force vector F = (2.0 i - 4.8 k) N
Compute the components of the magnetic field as follows:
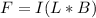
Replacing 8.6 A for I ; -2.0 j N for F & 2.3 m i for L
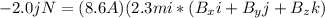
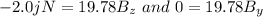
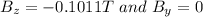
However in y direction ; we have :
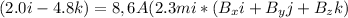
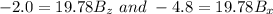
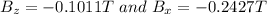
Hence, the component of magnetic field is as follows: