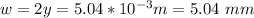Question

A beam of electrons is incident on a single slit that has a width of 1.00 × 10–6 m and a diffraction pattern is observed on a screen located 15.0 m from the slit. The momentum of an individual electron in the beam is 5.91 × 10–24 kg ⋅ m/s. What is the width of the central maximum fringe?

Answer 1

The width of the central maximum fringe in a single-slit diffraction pattern can be determined using the formula: width = (wavelength x distance to screen) / slit width. After calculating, the width of the central maximum fringe is approximately 3.17 × 10^5 m.

Step-by-step explanation:

The width of the central maximum fringe in a single-slit diffraction pattern can be determined using the formula:

width = (wavelength x distance to screen) / slit width

Using the given values, the width of the central maximum fringe can be calculated as:

width = (6.626 × 10^-34 kg⋅m²/s x 3.00 × 10^8 m/s x 15.0 m) / (5.91 × 10^-24 kg⋅m/s)

After calculating, the width of the central maximum fringe is approximately 3.17 × 10^5 m.

Answer 2

w = 5.04 mm

Step-by-step explanation:

To find the width of the central maximum you use the following formula for the height of the dark fringes:

`y=(m+(1)/(2))(\lambda D)/(d)` ( 1 )

y: height of the m-th dark fringe

λ: wavelength of the electron

D: distance to the screen = 15.0m

d: distance between slits = 1.00*10^{-6} m

twice the height of the first dark fringe (m = 1) gives you the width of the central peak.

You first calculate the wavelength of the electron by using the Broglie's relation:

`\lambda=(h)/(p_e)=(6.62*10^(-34)Js)/(5.91*10^(-24)kgm/s)\\\\\lambda=1.12*10^(-10)m`

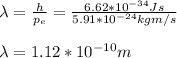
where you have used the constant's Planck h.

Next, you replace the values of the parameters in the equation ( 1 ) with m=1:

`y=(1+(1)/(2))((1.12*10^(-10)m)(15.0m))/(1.00*10^(-6)m)=2.52*10^(-3)m\\\\y=2.52\ mm`

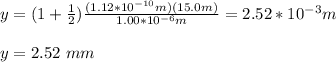
the width of the central maximum is:

`w=2y=5.04*10^(-3)m=5.04\ mm`