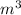Answer:
Volume of big locker = 0.36
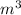
Volume of small locker = 0.18
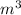
Total volume = 0.54
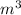
Explanation:
We are given the following:
Width of larger locker = 0.5 m
Depth of larger locker = 0.6 m
Height of larger locker = 1.2 m
It is a cuboid like structure and it is well known that Volume of a cuboid structure =
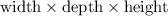
So, volume of larger locker =
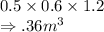
Width of smaller locker = 0.5 m
Depth of smaller locker = 0.6 m
Height of smaller locker =
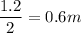
Volume of a cuboid structure =
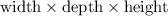
So, volume of smaller locker =
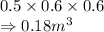
Adding both the volumes, Total volume = 0.54