Question

A catering service offers 5 appetizers,4 main courses, and 8 desserts. A customer is to select 4 appetizers,2 main courses,and 3 desserts for a banquet. In how many ways can this be done

Answer 1

468 ways

Explanation:

Given: A catering service offers 5 appetizers, 4 main courses, and 8 desserts

To find: number of ways a customer is to select 4 appetizers, 2 main courses,and 3 desserts.

Solution:

A permutation is an arrangement of elements such that order of elements matters and repetition is not allowed.

Number of appetizers = 5

Number of main courses = 4

Number of desserts = 8

Number of ways of choosing k terms from n terms =
`nPk=(n!)/((n-k)!)`

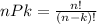
Number of ways a customer is to select 4 appetizers, 2 main courses,and 3 desserts =
`5P4+4P2+8P3`

`=(5!)/((5-4)!)+(4!)/((4-2)!)+(81)/((8-3)!)\\=5!+(4!)/(2!)+(8!)/(5!)\\=5!+(4* 3)+(8* 7* 6)\\=120+12+336\\=468`

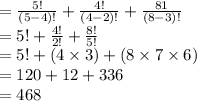
So, this can be done in 468 ways.