Answer:
a)
6.4 units
b)
56°
Explanation:
a)
A circle with circumference 8, has an arc with a 288 degree central angle. What is the length of the arc?
From geometry, we know that the length of an arc is the ratio of the central angle to 360° multiplied by the perimeter of the circle. Therefore:
length of arc =
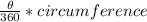 , where θ = central angle and circumference = 2πr
, where θ = central angle and circumference = 2πr
Substituting values:
length of arc =
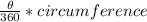 =
=
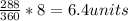
b)
Below are two parallel lines with a third line intersecting them.
The diagram is attached below.
Alternate Exterior Angles are a pair of angles formed on the outer side of each of those two lines when two lines are crossed by another line (the Transversal), but on opposite sides of the transversal.
From the diagram, x and 56° are Alternate Exterior Angles, therefore:
x = 56°