Answer:
6) b = 12mm
7) b = 24cm
Explanation:
6) To find b, you will subtract the square root of the square of 9mm from the square of 15mm
i.e. b =
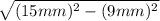
b =
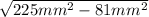
b =
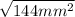
b = 12mm
7) To find b, you subtract the square root of the square of 10cm from the square of 26cm
i.e. b =
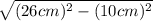
b =

b =
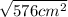
b = 24cm