Answer:
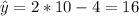
And the real value for this case is y=14. The residual is defined as:
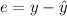
Replacing we got:
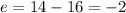
And the best answer would be:
-2
Explanation:
For this case we know that the best fit line for the relationship between x and y is given by:
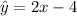
And we know that an individual in the dataset has a score of 10 on the x-variable and a score of 14 on the y-variable. So then we can find the estimated value like this:
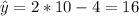
And the real value for this case is y=14. The residual is defined as:
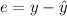
Replacing we got:
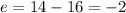
And the best answer would be:
-2