Answer:
28.6, that is, about 29 are expected to be defective
Explanation:
For each battery, there are only two possible outcomes. Either it is defective, or it is not. The probability of a battery being defective is independent of other betteries. So the binomial probability distribution is used to solve this question.
Binomial probability distribution
Probability of exactly x sucesses on n repeated trials, with p probability.
The expected value of the binomial distribution is:
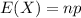
The probability that a battery is defective is 1/14.
This means that
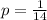
400 batteries.
This means that
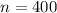
How many are expected to be defective?
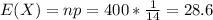
28.6, that is, about 29 are expected to be defective