Question

A school class went on a field trip to see a magician perform there were 17 females 20 males in the class the magicians randomly selected a volunteer from the audience in which had 52 females and 68 males given that the randomly selected audience member is a student from the class which equation can be used to find the probability p that the perdimos also a female?please help does anyone know the answer

Answer 1

alright, this is what I did.

p(a)=37/120

p(b)=17/37

p(anb)=(37/120)(17/37)=17/120

p(anb)/p(a)=17/120 divided by 37/120

=17/37

The probability of a person being picked being from the class and a female is 17/37.

Answer 2

P(B)= 17/20

Explanation:

Hello!

The audience of the magic show is conformed by a total of 120 people, 52 of which are female and 68 are men.

Within the audience there is a school class of 37, of these students, 17 are female and 20 are male.

If a random member of the audience is selected as a volunteer:

Let "A" represent the event that "the selected volunteer is a student of the class"

And "B" the event that "the selected student is female"

You have to calculate the probability of the selected volunteer being female, given that it is a member of the school class.

Symbolically:

P(B|A)

Using the formula of conditional probabilities you can calculate it as:

`P(B|A)= (P(AnB))/(P(A))`

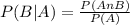
P(A∩B)=
`P(A)*P(B)= ((37)/(120) )*((17)/(20) )`=
`(629)/(2400)= 0.26`

`P(A)= (37)/(120) = 0.308`

`P(B|A)= (P(AnB))/(P(A))= (629/2400)/(37/120) = (17)/(20) = 0.85`

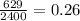
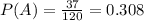
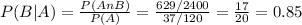
As you can see the probability of the event "The volunteer is female given that it was a student of the school class" means that you already know the selected volunteer was a student and only needed to calculate the probability of that student being female.

P(B)= 17/20

I hope this helps!