Answer:
1)
![[H^+]_(eq)=0.00029M](https://img.qammunity.org/2021/formulas/chemistry/college/kuvkf6xkmgshfsgd68eyrmlele2yw4u5pn.png)
2)
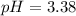
3)
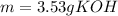
4)

Step-by-step explanation:
Hello,
1) Here, you should remember acetic acid dissociation is:
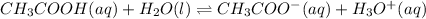
Thus, we propose the law of mass action for the aqueous species only:
![Ka=([CH_3COO^-][H_3O^+])/([CH_3COOH])](https://img.qammunity.org/2021/formulas/chemistry/college/x9gqcppr1cjs35u6uz54j6cm9iz4sh5osv.png)
Hence, in terms of the change
 due to reaction's extent we have:
due to reaction's extent we have:
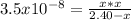
Solving for
 we obtain 0.00029 which equals the concentration of H⁺ or H₃O⁺ (they are the same) at equilibrium:
we obtain 0.00029 which equals the concentration of H⁺ or H₃O⁺ (they are the same) at equilibrium:
![[H^+]_(eq)=0.00029M](https://img.qammunity.org/2021/formulas/chemistry/college/kuvkf6xkmgshfsgd68eyrmlele2yw4u5pn.png)
2) As well as in the previous case, we write its equilibrium dissociation:
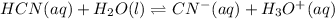
Thus, we propose the law of mass action for the aqueous species only:
![K=([CN^-][H_3O^+])/([HCN])](https://img.qammunity.org/2021/formulas/chemistry/college/lp436qnqgjo8ztdqu8js0lyt0gbs1g62ss.png)
Hence, in terms of the change
 due to reaction's extent we have:
due to reaction's extent we have:
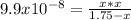
Solving for
 we obtain 0.000416 which equals the concentration of H⁺ or H₃O⁺ (they are the same) at equilibrium:
we obtain 0.000416 which equals the concentration of H⁺ or H₃O⁺ (they are the same) at equilibrium:
![[H^+]_(eq)=0.000416 M](https://img.qammunity.org/2021/formulas/chemistry/college/fu1d8ijrcztus76hj9qstey4y4kjgh22nu.png)
So we compute the pH:
![pH=-log([H^+]_(eq))=-log(0.000416)\\\\pH=3.38](https://img.qammunity.org/2021/formulas/chemistry/college/sj7i427tm01rlnm3fm1w29lqn37erhvww2.png)
3) In this case, from the formula defining molarity we first compute the moles of KOH whose molar mass is 56.1 g/mol considering the volume in litres:
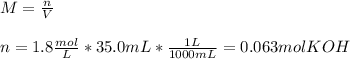
So we compute the grams by using its molar mass:
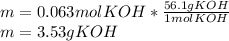
4) In this case, for this neutralization as both of them have one equivalent (one hydrogen in the acid and one hydroxyl in the base), we solve the following formula for the volume of KOH as the moles become equal at the equivalence:
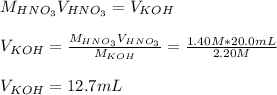
Best regards.