We have been given that Vicente has a prism-like water tank whose base area is 1.2 square meters. He bought 6 goldfish at the store, and the store owner told him to make sure their density in the tank isn't more than 4 fish per cubic meter.
First of all, we will find volume of water needed for 6 fishes using proportion.
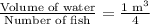
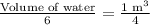
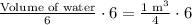

We know that volume of prism is base area times height.
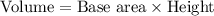
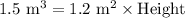

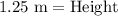
Therefore, the lowest possible height would be 1.25 meters.