Question

A geometric series G has common ratio r and an arithmetic series A has first term a and common difference d , where a and d are non–zero. The first three terms of G are equal to the third, fourth and sixth terms of A respectively. The sum of the first four terms of A is −6.

(a): Determine the least value of m such that the difference between the mth terms of G and A is more than 10000.

(b): Let an denote the nth term of A. The sequence xn is defined as xn = (2k)^a, where k is a constant. Find the range of values of k such that the series xn converges.

I have deduced that a=3, d=-3, r=2. Please help me solve (a) and (b).

Answer 1

1. m = 2.6×10⁻¹⁰

2. K < 1/2

Explanation:

The given parameters are;

For the GP = g, gr, gr²,.....,

AP = a, (a + d), (a + 2d), (a + 3d), (a + 4d), (a + 5d)

Therefore;

g = (a + 2d)

gr = (a + 3d)

gr² = (a + 5d)

Also a + (a + d) + (a + 2d) + (a + 3d) = 4a + 6d = -6

Therefore, a = (-6 - 6d)/4

Therefore, gr - g = (a + 3d) - (a + 2d) = d

g(1 - r) = d

g = d/(1 - r)

and gr/g = r = (a + 3d)/(a + 2d)

gr²/gr = r = (a + 5d)/(a + 3d)

Hence, (a + 5d)/(a + 3d) = (a + 3d)/(a + 2d)

Substituting the value of a from above, we have

`(7d -3)/(3d-3) = (3d -3)/(d-3)`

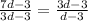
Which gives 2d² + 6d = 0

d = -3

Therefore, 4·a = -6 + 18 = 12

a = 3

g = -3

gr = -6

∴ r = 2

Therefore the term where the difference between the two terms is 10000 is found as follows;

`(-3)2^m - (3 + m * (-3)) = 10000`

`3m -3\cdot 2^m - 3 = 10000`

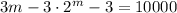
Therefore, 3·m - 3·2^m = 10003

Solving by computation, we have m = -2.6×10⁻¹⁰.

(b) For a sequence, xₙ = (2k)ᵃ

For convergence, (2k)ᵃ ÷ (2k)
`^(a+1)` <1

∴ 1/(2k) < 1

Hence 1/k < 2 or K < 1/2