Answer:
3.6
Explanation:
It can be seen from the diagram that ΔDAC and ΔABD are right angled triangle.
Using the SOH, CAH, TOA trigonometry identity on ΔDAC where;
AC is the hypotenuse = 5.1
CD is the opposite (since it faces the angle directly)
According to SOH;
Sin
 = opp/hyp
= opp/hyp
sin
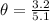
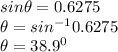
∠DAC = ∠BAD = 38.9°
According to ΔABD, the opposite side is DB which is unknown and the hypotenuse id AB i.e 5.7
Using SOH;
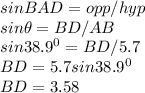
BD ≈ 3.6 to one dp