Question

use the limit theorem and the properties of limits to find the horizontal asymptotes of the graph of the function f(x)= 3x^2+5 / 4x^2-6x+2​

Answer 1

`y=(3)/(4)`

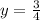
Explanation:

Given:
`f(x)=(3x^2+5)/(4x^2-6x+2)`

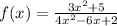
To find: horizontal asymptotes of the graph of the function

Solution:

Line y = L is a horizontal asymptote of the function y = f(x) if either
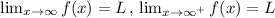`\lim_(x\rightarrow \infty )f(x)=L\,,\,\lim_(x\rightarrow \infty^+ )f(x)=L`, and L is finite

`f(x)=(3x^2+5)/(4x^2-6x+2)`

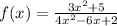
Use properties:

`\lim_(x\rightarrow a)(f+g)=\lim_(x\rightarrow a)f+\lim_(x\rightarrow a)g\\\lim_(x\rightarrow a)\left ( (f)/(g) \right )=(\lim_(x\rightarrow a)f)/(\lim_(x\rightarrow a)g)`

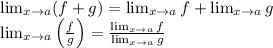
Divide numerator and denominator by
`x^2`

`f(x)=((3x^2+5)/(x^2))/((4x^2-6x+2)/(x^2))\\=(3+(5)/(x^2))/(4-(6)/(x)+(2)/(x^2))\\`

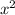
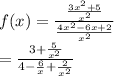
Therefore,

`\lim_(x\rightarrow \infty^- )\left [ (3+(5)/(x^2))/(4-(6)/(x)+(2)/(x^2)) \right ]`

`=(\lim_(x\rightarrow \infty^- ) \left [ 3+(5)/(x^2) \right ])/(\lim_(x\rightarrow \infty^- )\left [ 4-(6)/(x)+(2)/(x^2) \right ])\\=(3+0)/(4-0+0)\\=(3)/(4)`

Also,

`\lim_(x\rightarrow \infty^+ )\left [ (3+(5)/(x^2))/(4-(6)/(x)+(2)/(x^2)) \right ]=(\lim_(x\rightarrow \infty^+ ) \left [ 3+(5)/(x^2) \right ])/(\lim_(x\rightarrow \infty^+ )\left [ 4-(6)/(x)+(2)/(x^2) \right ])\\=(3+0)/(4-0+0)\\=(3)/(4)`

Here,
`\lim_(x\rightarrow \infty^- )\left [ (3+(5)/(x^2))/(4-(6)/(x)+(2)/(x^2)) \right ]=\lim_(x\rightarrow \infty^+ )\left [ (3+(5)/(x^2))/(4-(6)/(x)+(2)/(x^2)) \right ]=(3)/(4)`

So,
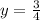`y=(3)/(4)` is the horizontal asymptote