Answer:
radius = 5
Explanation:
Question
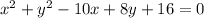
The equation of a circle is shown. What is the radius?
----------------------------------------------------------------------------------
Equation of a circle
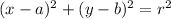
(where (a, b) is the center and r is the radius)
Given equation:
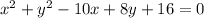
Collect like terms:
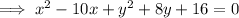
Subtract 16 from both sides:
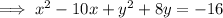
Complete the square for both variables.
Add 25 to both sides for x. Add 16 to both sides for y.
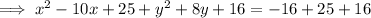
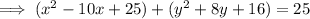
Factor the two variables:
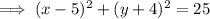
Therefore:
- center of the circle = (5, -4)
- radius of the circle = √25 = 5