Answer:
D.

Explanation:
Let's use the geometric sequence recursive formula:
 , where
, where
 is the nth term,
is the nth term,
 is the first term, and r is the common ratio.
is the first term, and r is the common ratio.
We see that since in the first month, Monique had $225 already, then that means
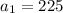 . We just need to find the common ratio. Let's use the information given about how much money she has in the sixth month. This means that
. We just need to find the common ratio. Let's use the information given about how much money she has in the sixth month. This means that
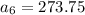 . Plug this into the formula to find r:
. Plug this into the formula to find r:

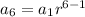
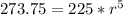
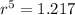
r ≈ 1.04
Thus, our formula is:
 , which is choice D.
, which is choice D.