Question

Rewrite the equation by completing the square x2-4x+3 = 0

Answer 1

x = 3, 1

Explanation:

x² - 4x + 3 = 0

First we need to subtract 3 from both sides of the equation.

x² - 4x = -3

Next, we need to take b (which is represented by -4 here) and plug it into the equation:
`((b)/(2)) ^(2)`

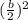
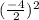`((-4)/(2) )^(2)` = (-2)²

Plug this into our equation.

x² - 4x + (-2)² = -3 + (-2)²

Simplify.

x² - 4x + (-2)² = -3 + (-2)²

x² - 4x + 4 = -3 + 4

x² - 4x + 4 = 1

Next we factor this.

x² - 4x + 4 = 1

(x - 2)(x - 2) = 1

(x - 2)² = 1

Now we solve for x. Take the square root of both sides.

√(x - 2)² = ±√1

x - 2 = ±√1

Square root of 1 is 1: √1 = 1

x - 2 = ±1

We're going to have two different solutions.

x - 2 = 1

x = 3

OR

x - 2 = -1

x = 1

Thus, x = 3, 1