Question

A person places $2150 in an investment account earning an annual rate of 3.3%, compounded continuously. Using the formula V = P e r t V=Pe rt , where V is the value of the account in t years, P is the principal initially invested, e is the base of a natural logarithm, and r is the rate of interest, determine the amount of money, to the nearest cent, in the account after 2 years.

Answer 1

Answer: 2296.69

If your reading this follow me on twitch mchammie to thank me for the right answer

Answer 2

We have been given that a person places $2150 in an investment account earning an annual rate of 3.3%, compounded continuously. We are asked to find the amount of money is the account after t years.

We will use continuous compound interest formula to solve our given problem.

`A=P\cdot e^(rt)`

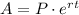
A = Final amount after t years,

P = Principal amount,

r = Annual interest rate in decimal form,

t = Time.

`r=3.3\%=(3.3)/(100)=0.033`

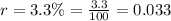
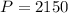`P=2150` and
`t=2`.

`A=2150\cdot e^(0.33\cdot 2)`

`A=2150\cdot e^(0.66)`

`A=2150\cdot 1.9347923344020315`

`A=4159.803518964`

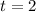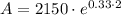
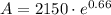
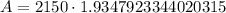
Upon rounding to nearest cent, we will get:

`A\approx4159.80`

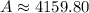
Therefore, there will be approximately $4159.80 in the account after 2 years.