Question

A prize wheel is divided into 12 equally likely spaces labeled 1 to 12.

Let E = {multiple of 3}

Let F = {even number}

Are the events E and Findependent?

Answer 1

Events E and F are independent.

Explanation:

E = {multiple of 3} = {3, 6, 9, 12}

P(E) = 4/12

F = {even number} = {2, 4, 6, 8. 10, 12}

P(F) = 6/12

E and F = {even and multiple of 3} = {6, 12}

P(E∩F) = 2/12

In order for two events to be independent the following relationship must be true:

`P(E)*P(F) = P(E\cap F)`

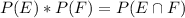
Testing this property:

`P(E)*P(F) = (4)/(12)*(6)/(12)=(24)/(144)=(1)/(6) \\P(E\cap F) = (2)/(12)=(1)/(6) \\P(E)*P(F) = P(E\cap F)`

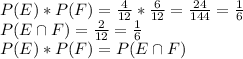
The relationship holds true, thus events E and F are independent.