Question

A random sample of 147 recent donations at a certain blood bank reveals that 87 were type A blood. Does this suggest that the actual percentage of type A donations differs from 40%, the percentage of the population having type A blood? Carry out a test of the appropriate hypotheses using a significance level of 0.01. State the appropriate null and alternative hypotheses.

Answer 1

Explanation:

Since we have given n = 157

x = 86

So,

`\hat{p}=(x)/(n)=(87)/(147)=0.59`

and we have p = 0.4

So, hypothesis would be

`H_0:p=\hat{p}\\\\H_a:p\\eq \hat{p}`

Since there is 1% level of significance.

So, test statistic value would be

`z=\frac{\hat{p}-p}{\sqrt{(p(1-p))/(n)}}\\\\z=\frac{0.59-0.40}{\sqrt{(0.4* 0.6)/(147)}}\\\\z=(0.19)/(0.0404)\\\\z=4.70`

Now we can calculate the p value with this probability:

=2*P(z>4.70)=0.00000203

The p value is lower than the significance level of 0.01

So, we reject the null hypothesis.

Hence, Yes, this suggest that the actual percentage of type A donations differs from 40%, the percentage of the population having type A blood.

Answer 2

`z=\frac{0.592 -0.4}{\sqrt{(0.4(1-0.4))/(147)}}=4.75`

`p_v =2*P(z>4.75)=0.000002034`

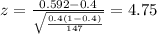
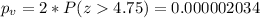
The p value is lower than the significance level of 0.01. So then we have enough evidence to reject the null hypothesis and we can conclude that the true proportion of type A donations differs from 40%, the percentage of the population having type A blood

Explanation:

Infomration given

n=147 represent the random sample taken

X=87 represent the people who are type A blood

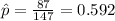`\hat p=(87)/(147)=0.592` estimated proportion of people with type A blood

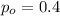`p_o=0.4` is the value to verify

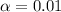`\alpha=0.01` represent the significance level

z would represent the statistic

`p_v` represent the p value

Hypothesis to test

We want to verify if type A donations differs from 40% so then the system of hypothesis are:

Null hypothesis:
`p=0.4`

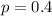
Alternative hypothesis:
`p \\eq 0.4`

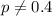
The statistic for this case is given:

`z=\frac{\hat p -p_o}{\sqrt{(p_o (1-p_o))/(n)}}` (1)

Replacing the info given we got:

`z=\frac{0.592 -0.4}{\sqrt{(0.4(1-0.4))/(147)}}=4.75`

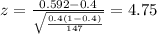
Now we can calculate the p value with this probability:

`p_v =2*P(z>4.75)=0.000002034`

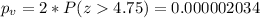
The p value is lower than the significance level of 0.01. So then we have enough evidence to reject the null hypothesis and we can conclude that the true proportion of type A donations differs from 40%, the percentage of the population having type A blood