Question

PLEASE HELP ME

Hartley has two 4-section spinners, each labeled 1-4. She will spin both spinners a total of 96 times. For each pair of numbers where the pointers of the spinners land on, Hartley will subtract the smaller number from the greater number.


1. How many possible total outcomes are there?


2. How many times should Hartley spin a difference of 1?


3. How many times should Hartley spin a difference of 0?

Answer 1

(1) The possible outcomes are: X = {0, 1, 2, 3}.

(2) The number of times should Hartley spin a difference of 1 is 36.

(3) The number of times should Hartley spin a difference of 0 is 24.

Explanation:

The number of sections on the spinner is 4 labelled as {1, 2, 3, 4}.

The total number of spins for each of the spinner is, n = 96.

(1)

The sample space of spinning both the spinners together are:

S = {(1, 1), (1, 2), (1, 3), (1, 4)

(2, 1), (2, 2), (2, 3), (2, 4)

(3, 1), (3, 2), (3, 3), (3, 4)

(4, 1), (4, 2), (4, 3), (4, 4)}

Total = 16.

The possible outcomes are:

X = {0, 1, 2, 3}.

(2)

The sample space with the difference 1 are:

S₁ = {(1, 2), (2, 1), (2, 3), (3, 2), (3, 4), (4, 3)}

n (S₁) = 6

The probability of the difference 1 is:

`P(\text{Diff}=1)=(n(S_(1)))/(N)=(6)/(16)=(3)/(8)`

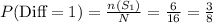
The spinners were spinner 96 times.

The expected number of times would Hartley spin a difference of 1 is:

`E(\text{Diff}=1)=P(\text{Diff}=1)* n\\\\=(3)/(8)* 96\\\\=36`

Thus, the number of times should Hartley spin a difference of 1 is 36.

(3)

The sample space with the difference 0 are:

S₂ = {(1, 1), (2, 2), (3, 3), (4, 4)}

n (S₂) = 4

The probability of the difference 0 is:

`P(\text{Diff}=0)=(n(S_(2)))/(N)=(4)/(16)=(1)/(4)`

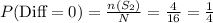
The spinners were spinner 96 times.

The expected number of times would Hartley spin a difference of 0 is:

`E(\text{Diff}=0)=P(\text{Diff}=0)* n\\\\=(1)/(4)* 96\\\\=24`

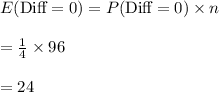
Thus, the number of times should Hartley spin a difference of 0 is 24.