Answer:
The time interval when
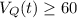 is at
is at
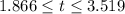
The distance is 106.109 m
Explanation:
The velocity of the second particle Q moving along the x-axis is :
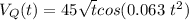
So ; the objective here is to find the time interval and the distance traveled by particle Q during the time interval.
We are also to that :
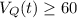 between
between
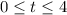
The schematic free body graphical representation of the above illustration was attached in the file below and the point when
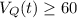 is at 4 is obtained in the parabolic curve.
is at 4 is obtained in the parabolic curve.
So,
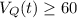 is at
is at
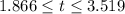
Taking the integral of the time interval in order to determine the distance; we have:
distance =
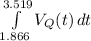
=
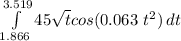
= By using the Scientific calculator notation;
distance = 106.109 m