Question

A set of average city temperatures in May are normally distributed with a mean of 20.66°C and a standard

deviation of 2 C. The average temperature of Singapore is 26°C!


What proportion of average city temperatures are lower than that of Singapore?


You may round your answer to four decimal places.



Round your answer to four decimal places

Answer 1

Answer: 0.9962

Explanation:

Answer 2

We have been given that a set of average city temperatures in May are normally distributed with a mean of 20.66°C and a standard deviation of 2 C. The average temperature of Singapore is 26°C. We are asked to find the proportion of average city temperatures that are lower than that of Singapore.

First of all, we will find z-score corresponding to sample score of 26.

`z=(x-\mu)/(\sigma)`, where,

z = z-score,

x = Random sample score,

`\mu` = Mean,

`\sigma` = Standard deviation.

`z=(26-20.66)/(2)`

`z=(5.34)/(2)`

`z=2.67`

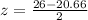
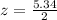
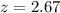
Now we need to find probability of a z-score less than 2.67 that is
`P(z<2.67)`.

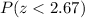Using normal distribution table, we will get:

`P(z<2.67)=0.99621`

Upon rounding to 4 decimal places, we will get:

`P(z<2.67)\approx 0.9962`

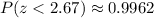
Therefore, approximately
`0.9962` of average city temperatures are lower than that of Singapore.