Question

A set of data is normally distributed with a mean of 28 and a standard deviation of 2. What is the probability that a value from the data is less than 22 or greater than 34?

a.

9%

c.

4.5%

b.

0.6%

d.

0.3%



Please select the best answer from the choices provided


A

B

C

D

Answer 1

`P(X<22)=P((X-\mu)/(\sigma)<(22-\mu)/(\sigma))=P(Z<(22-28)/(2))=P(z<-3)=0.00135`

`P(X>34)=P((X-\mu)/(\sigma)>(34-\mu)/(\sigma))=P(Z>(34-28)/(2))=P(z>3)=0.00135`

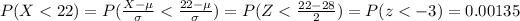
And if we add the two values we got 0.00135+0.00135 = 0.0027 and in % would be 0.27% and rounded would be 0.3 %

d. 0.3%

D

Explanation:

Let X the random variable that represent the variable of interest of a population, and for this case we know the distribution for X is given by:

`X \sim N(28,2)`

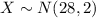
Where
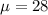`\mu=28` and
`\sigma=2`

We are interested on this probability

`P(X<22 \cup X>34)`

We can find the individual probabilities. We can use the z score formula given by:

`z=(x-\mu)/(\sigma)`

If we apply this formula to our probability we got this:

`P(X<22)=P((X-\mu)/(\sigma)<(22-\mu)/(\sigma))=P(Z<(22-28)/(2))=P(z<-3)=0.00135`

`P(X>34)=P((X-\mu)/(\sigma)>(34-\mu)/(\sigma))=P(Z>(34-28)/(2))=P(z>3)=0.00135`

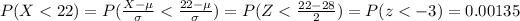
And if we add the two values we got 0.00135+0.00135 = 0.0027 and in % would be 0.27% and rounded would be 0.3 %

d. 0.3%

D