Question

URGENT!!

For triangle ABC, if the measure of angle A is 60° and the measure of angle B is 45°, and the measure of side b, opposite angle B, is 12cm, find, to the nearest tenth of a cm, the measure of side a.

A. 14.7cm
B. 9.8cm
C. 8.5cm
D. 17.0cm

Answer 1

A. 14.7 cm

Explanation:

To find the measure of side a, we will simply use the sine formula

`(sin A)/(a)` =
`(sin B)/(b)`

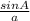where A,B are angles and a,b are sides of the triangle

from the question given, angle A = 60° angle B = 45° b = 12cm a = ?

`(sin 60)/(a)` =
`(sin 45)/(12)`

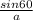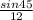
cross-multiply

a sin45 = 12 sin60

Divide both-side by sin 45

a = 12 sin 60/ sin45

a ≈ 14.7 cm

Answer 2

A. 14.7cm

Explanation:

In Triangle ABC

`\angle A=60^\circ\\\angle B=45^\circ\\b=12cm`

We are to determine the measure of side a.

Using Law of Sines

`(a)/(\sin A)= (b)/(\sin B)\\(a)/(\sin 60^\circ)= (12)/(\sin 45^\circ)\\\\$Cross multiply\\a*sin 45^\circ=12*\sin 60^\circ\\$Divide both sides by sin 45^\circ\\(a*sin 45^\circ)/(sin 45^\circ)= (12*\sin 60^\circ)/(\sin 45^\circ)\\\\a=14.7$ cm (to the nearest tenth of a cm)`

The correct option is A.