Answer:

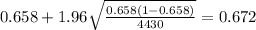
We ar confident that the true proportion of people in US who are obes is between 0.644 and 0.672
And the best option is given by:
(0.644, 0.672)
Explanation:
For this case we can begin calculating the proportion of people overweight with this formula:
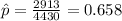
The confidence level is 95% , and the significance level would be given by
 and
and
 . And the critical value would be given by:
. And the critical value would be given by:
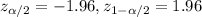
The confidence interval for the mean is given by the following formula:
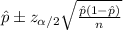
Replacing the info given we got:

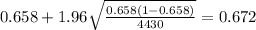
We ar confident that the true proportion of people in US who are obes is between 0.644 and 0.672
And the best option is given by:
(0.644, 0.672)