Question

A toy rocket is fired into the air from the top of a barn. It's height h in yards above the ground after t seconds is given by the function H(t)=-3t2+12t+24 what is the height of the barn? Include units! When did the rocket reach its maximum height? Include units what was the maximum height of the rocket? Include units

Answer 1

The rocket reached its maximum height at 2 seconds.

The maximum height of the rocket is 36 yards.

Explanation:

Quadratic equation:

In the format

`h(t) = ah^(2) + bh + c`

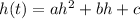
The maximum height happens at the instant of time:

`t_(v) = -(b)/(2a)`

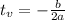
The maximu height is
`h(t_(v))`

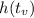
In this question:

`H(t) = -3t^(2) + 12t + 24`

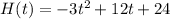
So
`a = -3, b = 12, c = 24`

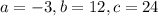
When did the rocket reach its maximum height?

`t_(v) = -(12)/(2*(-3)) = 2`

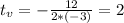
The rocket reached its maximum height at 2 seconds.

What was the maximum height of the rocket?

H(2).

`H(2) = -3*2^(2) + 12*2 + 24 = 36`

The maximum height of the rocket is 36 yards.