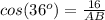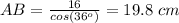Question

ABC is a right angled triangle .

AC= 16cm

Angle C = 90......



Plz plz plz plz plz plz help

Answer 1

ABC is a right-angled triangle.

AC= 16cm

Angle c= 90• (degrees)

Size of angle b: size of angle A = 3:2

Work out the length of AB

Give your answer to 3 significant figures.

`AB=19.8\ cm`

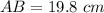
Explanation:

step 1

Find the measure of angle A

we know that

Triangle ABC is a right triangle

so

The sum of angle A plus angle B must be equal to 90 degrees by complementary angles

A+B=90⇒ equation A

`(B)/(A)=(3)/(2)`

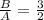
so

B=1.5A⇒ equation B

substitute equation B in equation A

A+1.5A=90

solve for A

`2.5A=90\\A=36^o`

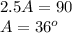
step 2

Find the length of side AB (hypotenuse)

we know that

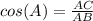`cos(A)=(AC)/(AB)` ⇒ by CAH (adjacent side divided by the hypotenuse)

substitute the given values

`cos(36^o)=(16)/(AB)`

`AB=(16)/(cos(36^o))=19.8\ cm`