Answer:
1)

The point estimate for the proportion of college graduates among women who work at home is 0.327
2)


The 80% confidence interval is given by (0.315; 0.339)
Explanation:
For this case we have the following info given:
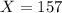 represent the women who worked at home who were college graduates
represent the women who worked at home who were college graduates
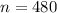 the sample size selected
the sample size selected
Part 1
In order to find the proportion of college graduates among women who work at home and we can use the following formula:
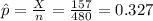
The point estimate for the proportion of college graduates among women who work at home is 0.327
Part 2
Construct an 80% confidence interval for the proportion of women who work at home who are college graduates. Round the answer to three decimal places. An 80% confidence interval for the proportion of women who work at home Is < p <
The confidence interval for the true proportion would be given by this formula
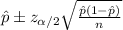
For the 80% confidence interval the value for the significance is
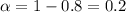 and
and
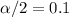 , the critical value would be given by:
, the critical value would be given by:
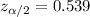
And replacing we goot:


The 80% confidence interval is given by (0.315; 0.339)