Question

According to a study done by the Gallup organization, the proportion of Americans who are satisfied with the way things are going in their lives is 0.82. Suppose a random sample of 100 Americans is asked the question "Are you satisfied with the way things are going in your life?" What is the probability the proportion of people who answer yes exceeds 0.85? Would it be unusual for a survey of 100 Americans to reveal that 75 or fewer are satisfiedwith the way things are going in their life?

Answer 1

0.217

Yes quite unusual ( See explanation )

Explanation:

Solution:-

- Denote among population ( P ) of the proportion of Americans who are satisfied with flow of their lives are p = 0.82.

- A random sample of n = 100 Americans were asked whether they are satisfied with the way things are going in your life.

- The sampling distribution of population proportion will be checked for normality as follows:

n = 100 , p^ = 0.82

- The requirements of normal distribution of sample proportion distribution:

n*p^ & n( 1 - p^ ) ≥ 10

n*p^*( 1 - p^ ) ≥ 10

- Verify the assumption of sample proportion to be normally distributed:

n*p^ = 100*0.82 = 82 ≥ 10

n*( 1 - p^ ) = 100*( 1 - 0.82 ) = 18 ≥ 10

n*p*( 1 - p^ ) = 100*0.82*( 1 - 0.82 ) = 14.76 ≥ 10

- Therefore, we can assume the sample proportion to be normally distributed as per Central Limit Theorem i.e sample is sufficiently large.

- Normal distribution of population proportion ( P ) is defined by two parameters that are defined as:

P ~ Norm ( μ_p , σ_p^2 )

Where,

μ_p: The mean of proportion

σ_p: The standard deviation of proportion

- The parameters for normally distributed sample proportion will be estimated using point estimation and point standard error estimation of sample population distribution.

Estimation:

μ_p = sample proportion = p^ = 0.82

σ_p =
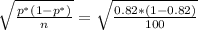`\sqrt{(p^*( 1 - p^* ))/(n) } = \sqrt{(0.82*( 1 - 0.82 ))/(100) }` = 0.03842

Hence,

P ~ Norm ( 0.82 , 0.03842^2 )

- The probability of proportion of people who answered yes to the survey question is greater than 0.85.

- We are to compute the probability of p ( P > 0.85 ) using the normal sample distribution of ( P ) determined above:

- The Z-score for the limiting value is:

Z = ( P - μ_p ) / σ_p

Z = ( 0.85 - 0.82 ) / 0.03842

Z = 0.78084

- Now using standard normal tables or normal calculator determine the corresponding probability:

p ( P > 0.85 ) = p ( Z > 0.78084 )

= 0.217439

Answer: The probability that at-least 85 people in the random sample of n = 100 Americans who answered " yes " to the survey question is 0.217.

- If x = 75 or fewer Americans say that they are satisfied with the way things are going in their life among a population of N = 100.

- The proportion ( P ) of the Americans that answered " yes " to the survey question:

P = x / N

P = 75 / 100 = 0.75

- Now we will compare the population proportion ( P ≤ 0.75 ) against the sampling distribution of ( P ). Compute the Z-score of the limiting value:

Z = ( P - μ_p ) / σ_p

Z = ( 0.75 - 0.82 ) / 0.03842

Z = -1.82196

- Now using standard normal tables or normal calculator determine the corresponding probability:

p ( P ≤ 0.75 ) = p ( Z ≤ -1.82196 )

= 0.03422543

Answer: This means that about 3.4 out of 100 random samples of size 100 will result in 75% or lower are satisfied with their life if the population proportion of Americans who are satisfied with their life is 0.82. Hence, p ( P < 0.75 ) = 3 is quite unusual from a survey of 100 Americans to show that less than 75% answered yes to the posed question.