Question

The rate of change of the number of mountain lions N(t) in a population is directly proportional to 725 - N(t), where t is the time in years. When t = 0, the population is 400. When t = 3, the population is 650. Find the population when t = 5. Round your answer to the nearest 50 mountain lions. a. Write the implied differential equation. b. Solve the equation to find the general solution. c. Use the given information to find a particular solution. d. Use the particular solution to answer the question.

Answer 1

a) The implied differential equation is
`(dN)/(725 - N) = kdt`

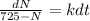
b) The general equation is
`N = 725 - C e^(-kt)`

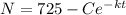
c) The particular equation is
`N = 725 - 325 e^(-0.49t)`

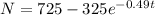
d) The population when t = 5, N(5) = 697 = 700( to the nearest 50)

Explanation:

The rate of change of N(t) can be written as dN/dt

According to the question,
`(dN)/(dt) \alpha (725 - N(t))`

`(dN)/(dt) = k (725 - N)\\(dN)/(725 - N) = kdt`

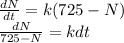
Integrating both sides of the equation

`\int {(1 )/(725 - N)} \, dN = \int {k} \, dt\\- ln (725 - N) = kt + C\\ ln (725 - N) = -(kt + C)\\725 - N = e^(-(kt + C)) \\725 - N = e^(-kt) * e^(-C) \\725 - N = C e^(-kt)\\N = 725 - C e^(-kt)`

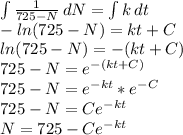
When t = 0, N = 400

`400 = 725 - C e^(-k*0)\\400 = 725 - C\\C = 725 - 400\\C = 325`

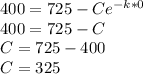
When t = 3, N = 650

`650 = 725 - (325 * e^(-3k))\\325 * e^(-3k) = 75\\e^(-3k) = 75/325\\e^(-3k) = 0.23\\-3k = ln 0.23\\-3k = -1.47\\k = 1.47/3\\k = 0.49`

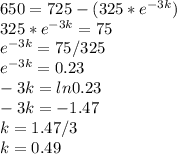
The equation for the population becomes:

`N = 725 - 325 e^(-0.49t)`

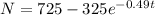
At t = 5, the population becomes:

`N = 725 - 325 e^(-0.49*5)\\N = 725 - 325 e^(-2.45)\\N = 696.95\\N(5) = 697`

N(5) = 700 ( to the nearest 50)