Question

Amir stands on a balcony and throws a ball to his dog, who is at ground level.

The ball's height (in meters above the ground), x seconds after Amir threw it, is modeled by

h(x)=-(x+1)(x-7)

What is the maximum height that the ball will reach?

Answer 1

16 meters

Explanation:

The height function is given by:

`h(x)=-(x+1)(x-7)\\h(x)=-(x^2+x-7x-7)\\h(x)=-x^2+6x+7`

The value of x, in seconds, for which the derivate of the height function is zero, is the time at which the maximum height occurs:

`(dh(x))/(dx)= h'(x)=-2x+6=0\\x=3`

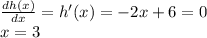
For x = 3 seconds, the height is:

`h(3)=-(3^2)+6*3+7\\h(3)=16\ m`

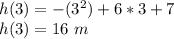
The maximum height that the ball will reach is 16 meters.