Question

An engineer wishes to determine the width of a particular electronic component. If she knows that the standard deviation of all components is 2.2 mm, how many of these components should she consider to be 80% sure of know the mean will be within 0.3 mm?

Answer 1

`n=((0.539(2.2))/(0.3))^2 =15.62 \approx 16`

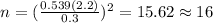
So the answer for this case would be n=16 rounded up to the nearest integer

Explanation:

For this case we have the following info given:

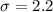`\sigma = 2.2` represent the population deviation

`Confidence =0.8`

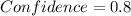
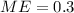`ME = 0.3` represent the margin of error desired

The margin of error for the true mean is given by this formula:

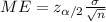`ME=z_(\alpha/2)(\sigma)/(√(n))` (a)

And on this case we have that ME =0.03 and we are interested in order to find the value of n, if we solve n from equation (a) we got:

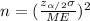`n=((z_(\alpha/2) \sigma)/(ME))^2` (b)

The confidence level is 80%, the significance would be
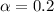`\alpha=0.2` and
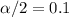`\alpha/2 =0.1` the critical value for this case is
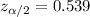`z_(\alpha/2)=0.539`, replacing into formula (b) we got:

`n=((0.539(2.2))/(0.3))^2 =15.62 \approx 16`

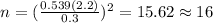
So the answer for this case would be n=16 rounded up to the nearest integer