Question

50 POINTSS!!! HELPPPPPPPPPP What are the solutions of the equation 9x4 – 2x2 – 7 = 0? Use u substitution to solve.

x = plus-or-minus StartRoot seven-ninths EndRoot and x = ±1
x = plus-or-minus StartRoot seven-ninths EndRoot and x = ±i
x = plus-or-minus i StartRoot seven-ninths EndRoot and x = ±1
x = plus-or-minus i StartRoot seven-ninths EndRoot and x =

Answer 1

Answer: C

Explanation:

just did this

Answer 2

C. x = ±i√7/9 OR x = ±1

Explanation:

We want to use u-substitution to solve this. This basically means that we substitute u for a certain expression / value that will make it easier to solve the problem.

Our equation is
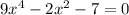`9x^4-2x^2-7=0`. This is a quartic, which we're not that familiar with, so let's try to turn it into a quadratic. Set u equal to x² and substitute that in:

`9(x^2)^2-2(x^2)-7=0`

`9u^2-2u-7=0`

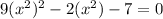
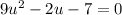
Ah, now we can easily factor this. It becomes:

(9u + 7)(u - 1) = 0

u = -7/9 or u = 1

Now, substitute these into u = x² to solve for x:

u = x²

-7/9 = x²

x = ±√-7/9 = ±i√7/9

OR

u = x²

1 = x²

x = ±1