Answer:
C. x = ±i√7/9 OR x = ±1
Explanation:
We want to use u-substitution to solve this. This basically means that we substitute u for a certain expression / value that will make it easier to solve the problem.
Our equation is
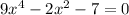 . This is a quartic, which we're not that familiar with, so let's try to turn it into a quadratic. Set u equal to x² and substitute that in:
. This is a quartic, which we're not that familiar with, so let's try to turn it into a quadratic. Set u equal to x² and substitute that in:

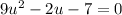
Ah, now we can easily factor this. It becomes:
(9u + 7)(u - 1) = 0
u = -7/9 or u = 1
Now, substitute these into u = x² to solve for x:
u = x²
-7/9 = x²
x = ±√-7/9 = ±i√7/9
OR
u = x²
1 = x²
x = ±1