Question

Based on historical data, your manager believes that 26% of the company's orders come from first-time customers. A random sample of 158 orders will be used to estimate the proportion of first-time-customers. What is the probability that the sample proportion is greater than than 0.4?

Note: You should carefully round any z-values you calculate to 4 decimal places to match wamap's approach and calculations.



Answer =


(Enter your answer as a number accurate to 4 decimal places.)

Answer 1

`\hat p \sim N( p, \sqrt{(p (1-p))/(n)})`

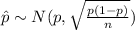
And we can use the z score formula given by:

`z = (\hat p -\mu_p)/(\sigma_p)`

And if we find the parameters we got:

`\mu_p = 0.26`

`\sigma_p = \sqrt{(0.26(1-0.26))/(158)} = 0.0349`

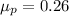
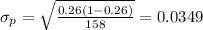
And we can find the z score for the value of 0.4 and we got:

`z = (0.4-0.26)/(0.0349)= 4.0119`

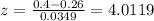
And we can find this probability:

`P(z>4.0119) = 1-P(z<4.0119)`

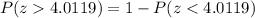
And if we use the normal standard table or excel we got:

`P(z>4.0119) = 1-P(z<4.0119)=1-0.99997 = 0.00003`

Explanation:

For this case we have the following info given:

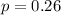`p = 0.26` represent the proportion of the company's orders come from first-time customers

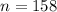`n=158` represent the sample size

And we want to find the following probability:

`p(\hat p >0.4)`

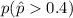
And we can use the normal approximation since we have the following two conditions:

1) np = 158*0.26 = 41.08>10

2) n(1-p) = 158*(1-0.26) = 116.92>10

And for this case the distribution for the sample proportion is given by:

`\hat p \sim N( p, \sqrt{(p (1-p))/(n)})`

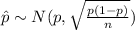
And we can use the z score formula given by:

`z = (\hat p -\mu_p)/(\sigma_p)`

And if we find the parameters we got:

`\mu_p = 0.26`

`\sigma_p = \sqrt{(0.26(1-0.26))/(158)} = 0.0349`

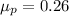
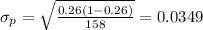
And we can find the z score for the value of 0.4 and we got:

`z = (0.4-0.26)/(0.0349)= 4.0119`

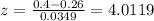
And we can find this probability:

`P(z>4.0119) = 1-P(z<4.0119)`

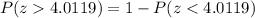
And if we use the normal standard table or excel we got:

`P(z>4.0119) = 1-P(z<4.0119)=1-0.99997 = 0.00003`