Question

How many real solutions does the equation 8x^2 − 10x + 15 = 0 have?

A)No real solution
B)One Real solution
c)Two Solutions
D)More than two real solutions
Thanks

Answer 1

The correct option is (A) No real solution.

Explanation:

The expression provided is a quadratic equation.

`8x^(2)-10x+15=0`

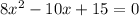
The roots of a quadratic equation are:

`x = ( -b \pm √(b^2 - 4ac))/( 2a )`

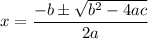
Here,

a = 8

b = -10

c = 15

The conditions to determine real and complex roots are:

• If
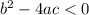  `b^(2)-4ac<0` then the quadratic equation has two complex roots.
• If
  `b^(2)-4ac>0` then the quadratic equation has two real roots.

Compute the value of
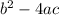`b^(2)-4ac` as follows:

`b^(2)-4ac=(-10)^(2)-(4* 8*15)\\\\`

`=100-480\\=-380\\<0`

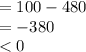
The equation has two complex roots.

Thus, the correct option is (A).