Question

Given a polynomial and one of its factors bother main factors 9x^3 + 20x^2 - 68x - 16; (x+4)

Answer 1

9x+2 and x-2.

Explanation:

Given the polynomial
`9x^3 + 20x^2 - 68x - 16`

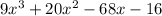
If one of the factors is x+4, then to obtain the other factor, we divide the polynomial by the known factor.

`(9x^3 + 20x^2 - 68x - 16)/(x+4) =9x^2-16x-4`

Next, we factorize our result

`9x^2-16x-4=9x^2-18x+2x-4\\=9x(x-2)+2(x-2)\\=(9x+2)(x-2)`

Therefore, the other factors of the polynomial are 9x+2 and x-2.