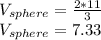Question

A sphere and a cylinder have the same radius and height. The volume of the cylinder is 11 ft.

h
Which equation gives the volume of the sphere?

Answer 1

C

Explanation:

Answer 2

`V_(sphere)=(2V_(cylinder))/(3)`

`V_(sphere)=7.33`

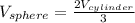
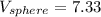
Step-by-step explanation:

Information we have:

Volume of the cylinder:
`11ft`

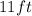
The formula for volume of a cylinder is:

`V_(cylinder)=\pi r^2h`

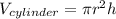
where
`r` is the radius and and h is the height

and the formula for the volume of a sphere is:

`V_(sphere)=(4\pi r^3)/(3)`

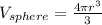
we dont have the height of the sphere in the formula but the height is double the radius:

`h=2r`

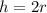
thus we manipulate the formula for the volume to get a 2r and the substitute with h:

`V_(sphere)=(2*2\pi r^2*r)/(3) \\V_(sphere)=(2\pi r^2(2r))/(3)`

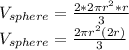
and we substitute that
`h=2r`

`V_(sphere)=(2\pi r^2h)/(3)`

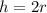
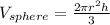
the value
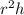`r^2h` must be equal for the sphere and for the cylinder.

We clear
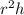`r^2h` from the volume of the cylinder

`V_(cylinder)=\pi r^2h`

• 
  `r^2h=(V_(cylinder))/(\pi)`

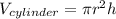
and we do the same for the volume of the sphere:

`V_(sphere)=(2\pi r^2h)/(3)`

• 
  `r^2h=(3V_(sphere))/(2\pi)`

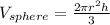
and we equal these two values for
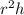`r^2h` since we are told the radius and the height are the same:

`(V_(cylinder))/(\pi)=(3V_(sphere))/(2\pi)`

and finally, we clear for the volume of the sphere:

`V_(sphere)=(V_(cylinder)*2\pi)/(3\pi) \\V_(sphere)=(2V_(cylinder))/(3)`this is the general expression.

and considering the volume of the cylinder is 11ft:

`V_(sphere)=(2*11)/(3)\\ V_(sphere)=7.33`