Answer:
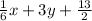 or x + 18y + 39
or x + 18y + 39
Explanation:
 =
=

→ First multiply everything by 2 to get rid of the fraction
3y = 6x - 12
→ We want to find the equation that's parallel to this line and passes through (3 , 2). The first thing we know about parallel lines is that the gradient is the negative reciprocal so,

→ Now we substitute in the values (3 , 2)
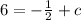
→ Add
 to both sides to isolate c
to both sides to isolate c
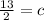
So the equation of the line that is parallel to
 =
=
 is
is
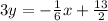 but we are not finished we are asked to but the equation in the format
but we are not finished we are asked to but the equation in the format
ax + by + c = 0 so,
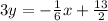
Rearrange
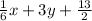
If the question want's the answer in whole numbers then multiply everything by 6
x + 18y + 39