 The sum of the Squares of three consecutive number is 110. Then determine the Three Numbers.
The sum of the Squares of three consecutive number is 110. Then determine the Three Numbers.
So, First of all The Question is to find out three consecutive Numbers .
First of all let's learn a little about Consecutive Numbers. So, Consecutive Numbers are the Numbers which follows each other. For example :- 1,2,3,4 are consecutive Numbers.
Let's start with Our Question :-
- Let The First consecutive number be = x
- and second number be = x + 1
- Third number be = x + 2
So,

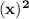 +
+
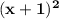 +
+
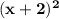 =
=
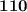

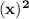 +
+
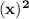 +
+
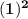 +
+
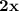 +
+
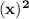 +
+
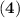 +
+
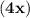 =
=
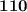

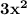 +
+
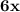 +
+
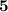 -
-
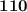 =
=

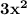 +
+
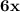 -
-
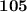 =
=
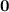
By taking 3 Out as Common, we are left with the Quadratic Equation :—

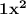 +
+
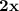 -
-
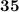 =
=
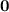
By Using Quadratic Formula,
x = -b ± √(b)^2— 4 × a × c / 2a
x = -2 ± √(2)^2— 4 × 1 × -35 / 2×1
x = -2 ± √144/2
[ As we know that "144" is square of 12 ]
x = -2 ± 12/2
- Taking Positive
- x = -2+12/2
- x = 5
Hence, x = +5
x +1 = 5+1 = +6
x+2 = 5+2 = +7
- Taking Negative sign
- x = -2-12/2
- x = -7
Hence, x = -7
x+1 = -7+1 = -6
x+2 = -7+2 = -5
Hence, The Three consecutive Numbers are ±5,±6,±7.