Answer:
The probability that the first card chosen is club and second card chosen is of heart is .
Explanation:
Total number of cards in the deck is 52 (total number of cases).
Probability of an event E can be formulated as:
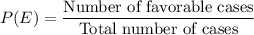
For event A, number of cards of type club = 13 (favorable cases)
So,
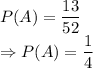
For event B, number of cards of type heart = 13 (favorable cases)
So,
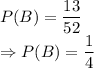
It is given that card is replaced before choosing the second card.
These events A and B are independent events, happening of one event does not effect the happening of other. And probability of both happening together can be found as following:
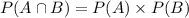

The probability that the first card chosen is club and second card chosen is of heart is
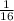 .
.