Answer:
Sin A =
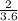
Cos A =
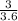
Tan A =

Explanation:
First of all, we will need to find the hypotenuse. We can do this using the Pythagoras theorem.
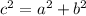
where a = 2 and b = 3,
solving for c we end up with 3.6.
Sin A =
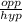
Cos A =
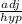
Tan A =
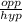
The line opposite to the angle A is 2 and the line adjacent to it is 3.
Filling in, we get the answer.
Hope this helps.