Question

The ages of 11 students enrolled in an on-line macroeconomics course are given in the following steam-and-leaf display:

Stem Leaf
----- -----------------------
1 9 9
2 1 5 5 8 9
3 0 1 2
4 0
Here 1|9 implies 19 years (i.e. the stem represents tens and leaf represents units).

The standard deviation of the age distribution is years. [Answer up to four digits after decimal]

Incorrect. Tries 2/3 Previous Trie

Answer 1

The standard deviation of the age distribution is 6.2899 years.

Explanation:

The formula to compute the standard deviation is:

`SD=\sqrt{(1)/(n)\sum\limits^(n)_(i=1){(x_(i)-\bar x)^(2)}}`

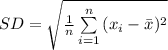
The data provided is:

X = {19, 19, 21, 25, 25, 28, 29, 30, 31, 32, 40}

Compute the mean of the data as follows:

`\bar x=(1)/(n)\sum\limits^(n)_(i=1){x_(i)}`

`=(1)/(11)* [19+19+21+...+40]\\\\=(299)/(11)\\\\=27.182`

Compute the standard deviation as follows:

`SD=\sqrt{(1)/(n)\sum\limits^(n)_(i=1){(x_(i)-\bar x)^(2)}}`

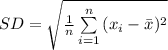
`=\sqrt{(1)/(11-1)* [(19-27.182)^(2)+(19-27.182)^(2)+...+(40-27.182)^(2)]}}\\\\=\sqrt{(395.6364)/(10)}\\\\=6.28996\\\\\approx 6.2899`

Thus, the standard deviation of the age distribution is 6.2899 years.