Answer:
Indeed, the two samples should contain about the same number of gas particles. However, the molar mass of
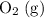 is larger than that of
is larger than that of
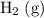 (by a factor of about
(by a factor of about
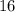 .) Therefore, the mass of the
.) Therefore, the mass of the
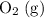 sample is significantly larger than that of the
sample is significantly larger than that of the
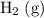 sample.
sample.
Step-by-step explanation:
The
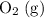 and the
and the
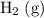 sample here are under the same pressure and temperature, and have the same volume. Indeed, if both gases are ideal, then by Avogadro's Law, the two samples would contain the same number of gas particles (
sample here are under the same pressure and temperature, and have the same volume. Indeed, if both gases are ideal, then by Avogadro's Law, the two samples would contain the same number of gas particles (
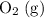 and
and
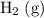 molecules, respectively.) That is:
molecules, respectively.) That is:
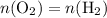 .
.
Note that the mass of a gas
 is different from the number of gas particles
is different from the number of gas particles
 in it. In particular, if all particles in this gas have a molar mass of
in it. In particular, if all particles in this gas have a molar mass of
 , then:
, then:
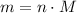 .
.
In other words,
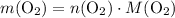 .
.
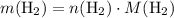 .
.
The ratio between the mass of the
 and that of the
and that of the
 sample would be:
sample would be:
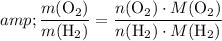 .
.
Since
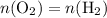 by Avogadro's Law:
by Avogadro's Law:
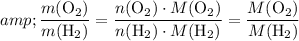 .
.
Look up relative atomic mass data on a modern periodic table:
Therefore:
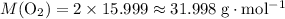 .
.
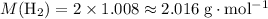 .
.
Verify whether
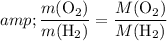 :
:
- Left-hand side:
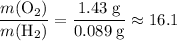 .
. - Right-hand side:
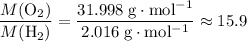 .
.
Note that the mass of the
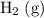 sample comes with only two significant figures. The two sides of this equations would indeed be equal if both values are rounded to two significant figures.
sample comes with only two significant figures. The two sides of this equations would indeed be equal if both values are rounded to two significant figures.