Question

The mean potassium content of a popular sports drink is listed as 145 mg in a 32-oz bottle. Analysis of 26 bottles indicates a sample mean of 144.4 mg. (a) State the hypotheses for a two-tailed test of the claimed potassium content. H0: μ = 145 mg vs. H1: μ ≠ 145 mg H0: μ ≤ 145 mg vs. H1: μ > 145 mg H0: μ ≥ 145 mg vs. H1: μ < 145 mg a b c (b) Assuming a known standard deviation of 2.9 mg, calculate the z test statistic to test the manufacturer’s claim. (Round your answer to 2 decimal places. A negative value should be indicated by a minus sign.) Test statistic (c) At the 10 percent level of significance (α = .10) does the sample contradict the manufacturer’s claim? Decision Rule: Reject H0 The sample the manufacturer's claim. (d) Find the p-value. (Round intermediate calculations to 2 decimal places. Round your answer to 4 decimal places.) p-value

Answer 1

Explanation:

Given that,

Sample size n= 26

Sample mean = 144.4mg

Population standard deviation = 2.9mg

a) Null and alternative hypothesis are

H₀ : μ = 145mg vs H₁ : μ ≠ 145mg

b) Test statistic is

`Z=(\bar x-u)/(\sigma/√(n) ) \\\\Z = (144.4-145)/(2.9/√(26) ) \\\\=-1.05`

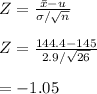
c) the critical values at

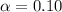`\alpha = 0.10` are
`Z_(\alpha /2)= \pm 1.645`

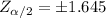
Since it is two-tailed test

Decision rule: reject H₀

If Z > +1.645 or if Z < -1.645

Here Z = - 1.05 > - 1.645

⇒ we fail to reject H₀

⇒ the sample does not contradict the manufacturers claim

d) P-value = 2* P( Z < -1.05)

= 2 * 0.1469

= 0.2938

⇒ P-value = 0.2938