Question

A study is being conducted in which the health of two independent groups of ten policyholders is being monitored over a one-year period of time. Individual participants in the study drop out before the end of the study with probability 0.2 (independently of the other participants). Calculate the probability that at least nine participants complete the study in one of the two groups, but not in both groups?

Answer 1

46.91% probability that at least nine participants complete the study in one of the two groups, but not in both groups

Explanation:

We use two binomial trials to solve this question.

Binomial probability distribution

The binomial probability is the probability of exactly x successes on n repeated trials, and X can only have two outcomes.

`P(X = x) = C_(n,x).p^(x).(1-p)^(n-x)`

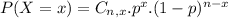
In which
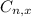`C_(n,x)` is the number of different combinations of x objects from a set of n elements, given by the following formula.

`C_(n,x) = (n!)/(x!(n-x)!)`

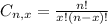
And p is the probability of X happening.

Probability of at least nine participants finishing the study in a group.

0.2 probability of a students dropping out. So 1 - 0.2 = 0.8 probability of a student finishing the study. This means that
`p = 0.8`.

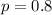10 students, so
`n = 10`

We have to find:

`P(X \geq 9) = P(X = 9) + P(X = 10)`

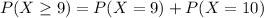
Then

`P(X = x) = C_(n,x).p^(x).(1-p)^(n-x)`

`P(X = 9) = C_(10,9).(0.8)^(9).(0.2)^(1) = 0.2684`

`P(X = 10) = C_(10,10).(0.8)^(10).(0.2)^(0) = 0.1074`

`P(X \geq 9) = P(X = 9) + P(X = 10) = 0.2684 + 0.1074 = 0.3758`

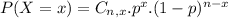
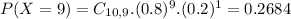
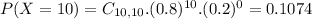
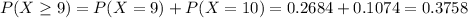
0.3758 probability that at least nine participants complete the study in a group.

Calculate the probability that at least nine participants complete the study in one of the two groups, but not in both groups?

0.3758 probability that at least nine participants complete the study in a group. This means that
`p = 0.3758`

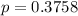
Two groups, so
`n = 2`

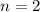
We have to find P(X = 1).

`P(X = x) = C_(n,x).p^(x).(1-p)^(n-x)`

`P(X = 2) = C_(2,1).(0.3758)^(1).(0.6242)^(1) = 0.4691`

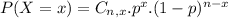
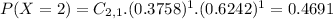
46.91% probability that at least nine participants complete the study in one of the two groups, but not in both groups

Answer 2

Explanation:

Assume that X and Y are the number of people who the survey in first and second groups respectively.

The probability of at least 9 participants complete the survey in one of the two groups , but not in both is

[X ≥ 9, Y ≤ 8 or X ≤ 8, Y ≥ 9] = P ( X ≥ 9) P(Y ≤ 8) + P ( X ≤ 8) P(Y ≥ 9)

Since the distribution in the two groups are same, so

P(X ≤ 8) = P(Y ≤ 8) and P(X ≥ 9) = P(Y ≥ 9)

Thus,

P(X ≥ 9) P(Y ≤ 8) + P(X ≤ 8) P(Y ≥ 9) = P(X ≥ 9)P(Y ≤ 8) + P( X ≤ 8)P(X ≥9)

= 2 P(X ≥ 9)P(X ≤ 8)

P(X ≥ 9)P(Y ≤ 8) + P(X ≤ 8)P(Y ≥ 9) = 2 P(X ≥ 9)(1 - P(X ≥ 9)) -----(1)

Since,

P(X ≤ 8) = 1 - P(X ≥ 9)

Here,n = 10, P = 0.8 and X = 9 and 10

P(x ≥ 9) = P(a) + P(10)

`= \left(\begin{array}{ccc}10\\9\end{array}\right)(0.8)^9(0.2)^1+\left(\begin{array}{ccc}10\\10\end{array}\right)(0.8)^1^0(0.2)^0\\\\=0.3758`

Substitute P(X ≥ 9) = 0.3758 in eqn(1)

P( X ≥ 9 )P(Y ≤ 8) + P(X ≤ 8)P(Y ≥ 9) = 2 * 0.3758(1 - 0.3758)

= 0.7516(0.6242)

= 0.469

Therefore, the probability of at least 9 participants complete the study in one of the two groups but not in both the group is

(0.3758)(0.6242) + (0.6242)(0.3758)

= 0.469g