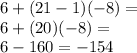Question

For the following arithmetic sequence, find the 21st term and write the explicit equation 6,-2,-10,-18... find a21

Answer 1

`A_(21)=-154`

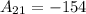
Explanation:

We are going to use the general sequence equation in order to figure out our "nth term" of the sequence.

General sequence equation (not given in UK formula booklet, need to know):

`A_n=A_1+(n-1)d`

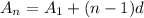
For the first term, we substitute in n as one:

`A_1=A_1+(1-1)d\\A_1=6`

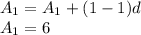
For the second term, n is two:

`A_2=6+(2-1)d`

`-2=6+d`

`d=-8`

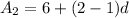
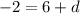
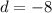
Verify for the third term

`6+(3-1)(-8)=-10`

`6+2(-8) = -10`

`6-16=-10`

`-10=-10`

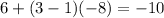
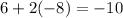
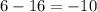
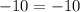
This is correct.

Substitute in for the twenty-first term:

`6+(21-1)(-8)=\\6+(20)(-8)=\\6-160=-154`