Question

There were million licensed drivers in the US in 2000 and million in 2010.1 (a) Find a formula for the number, , of licensed drivers in the US as a function of , the number of years since 2000, assuming growth is linear. MathPAD Response msnViewer_EAT_1405972601180_1_8980000476313852_mathpad_7_svg ViewEdit millions (b) Find a formula for the number, , of licensed drivers in the US as a function of , the number of years since 2000, assuming growth is exponential. Round your answer for the base to four decimal places.

Answer 1

a) N = 1.9t + 191 millions

b) N = 191 × (1.00952852)ˣ

Explanation:

a)

For a linear function; we use the expression:

y = mx + c

where;

m = slope (i.e when two points of model are given (x₁,y₁) and (x₂,y₂);

Thus;

`m = (y_2-y_1)/(x_2-x_1)`

c = intercept of y or the value of y when x = 0

So , let assume that we take year since 2000 as t .so that t=0 means 2000 ,t=5 means 2005 and t=10 means 2010 etc

now number of licensed driver is N and related to t linearly

Thus;

N = mt + c (1)

GIVEN THAT:

At 2000 ,when t=0 number of licensed driver is 191 million ,so N intercept (N value when x=0) is 191

The number of values of drivers is 191 million in 2000 (t=0)

and 210 million in in 2010(t=10). So to points in the model is (0,191) and (10,210)

However; the slope m can now be illustrated as :

Slope
`m = (210-191)/(10-0)`

`m = (19)/(10)`

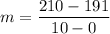
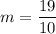
m = 1.9

Now substituting the value of c and m to the above linear model ; we have:

N = 1.9t + 191 millions

b)

An exponential model have standard equation
`\mathbf{y=ab^x}`

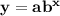
here :

a is the value of y when x=0 and b is the base of exponential function

when a value of y other than for x=0 is known we can calculate b by just substituting and solving

we have N as exponential function of year t

Therefore;
`\mathbf{N= ab^t}`

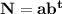
Thus; if we take year since 2000 as t so that t=0 means 2000, t=10 means 2010 ....etc

At t=0 we have N=191 so a=191

so our exponential function is :

`\mathbf{N= 191b^t}`

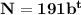
we know that at t=10 at 2010 ,N is 210;

then replacing all value and solving for b ; we have

`\mathbf{210= 191b^(10)}`

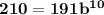
Making b the subject of the formula by rearrangement ; we have :

`\mathbf{b^(10) = (210)/(191)}`

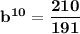
Taking log of both sides;

`\mathbf{log_(10) \ b^(10) = log_(10) \ ((210)/(191))}`

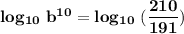
we know log
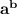`\mathbf{a^b}` =b log a

`\mathbf{10*log_(10) b =log_(10) (210)/(191)}`

`\mathbf{log_(10) b = (0.41185927)/(10)}`

`\mathbf{log_(10) b = {0.041185927}}`

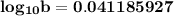
Taking exponential with base 10 on both side

`\mathbf{10^{log_(10) \ b } = 10^(0.041185927)}`

`\mathbf{b } = 10^(0.041185927)}`

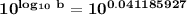
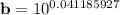
b = 1.00952852

Hence; our exponential model is :

N = 191 × (1.00952852)ˣ